DCF Series: Discounting FCF by calculating WACC

After projecting Free Cash Flow, the next step is to discount it back to the present value. In this post, we discuss how to do this - focusing on calculating the Weighted Average Cost of Capital (or WACC)

This is part of the DCF Valuation series; if you haven't read any of the previous posts, start here.

---

What is WACC?

WACC, or Weighted Average Cost of Capital, is a measure of how much it cost the company to raise the capital that it uses. You can think of it as the 'opportunity cost' for investors. By investing in this company, they passed on the opportunity to make money through other means — the WACC represents the potential returns of those 'other opportunities', to get an idea of what returns would be considered satisfactory to investors of the company.

Calculating WACC

Companies can raise money from two sources: either through debt, or through equity (i.e. selling shares in the company to investors).

Usually, it's both.

To find the WACC, we'll need to calculate the WACC for both of these sources, in proportion to how much of each was raised:

$$\text{WACC}\text{overall} = r\text{equity} * \text{WACC}\text{equity} + r\text{debt} * \text{WACC}_\text{debt}$$

and where:

$$r_\text{equity} = \frac{\text{Equity capital raised}}{\text{Total capital raised}}$$ and $$r_\text{debt} = \frac{\text{Debt capital raised}}{\text{Total capital raised}}$$

By using ratios, we ensure that $$$\text{WACC}_\text{overall}$$$represents the true cost of capital — accounting for both equity and debt in proportion to the amount raised through each instrument.

By reviewing the SFIX's 10-K Annual filing, we can find the figures we need in the Balance Sheet:

Debt Capital raised is the equivalent of Current Operating lease liabilities + Operating lease liabilities, net of current portion = 24,333 + 140,175 = $164,508 (in thousands) = $164,508,000

Equity Capital raised is simply the market cap of the company. You can get this on Yahoo! Finance on the stock page of the company (or just multiply the total number of outstanding shares, by the current stock price). That gives us: $6.484bn = $6,484,000,000

Total Capital raised = Debt + Equity = $164,508,000 + $6,484,000,000 = $6,648,508,000

The ratios are therefore:

$$r_\text{equity} = \frac{\text{Equity capital raised}}{\text{Total capital raised}} = \frac{6,484,000,000}{6,648,508,000} = 97.5%$$ $$r_\text{debt} = \frac{\text{Debt capital raised}}{\text{Total capital raised}} = \frac{164,508,000}{6,648,508,000} = 2.5%$$

The question now becomes, how do we calculate $$$\text{WACC}\text{equity}$$$ and $$$\text{WACC}\text{debt}$$.

Calculating $$$\text{WACC}_\text{debt}$$$

We'll start with calculating $$$\text{WACC}_\text{debt}$$$, since it's easier to follow :)

Since debt almost always carries interest expense², you'd think we could easily calculate the cost of debt using $$$\text{WACC}_\text{debt} = \frac{\text{Interest Expense}}{\text{Total Debt Raised}}$$$.

However, there's one more consideration we have not accounted for! In most countries, interest expenses are tax-deductible. That means the true cost of debt is actually lower than this figure would suggest.¹

To account for the tax-deductions resulting from interest expenses, we first need to find out what the 'effective tax rate' for the company is:

$$\text{Effective Tax Rate (t)} = \frac{\text{Income Tax Expense}}{\text{Income Before Tax}}$$

This is the % of income the company is actually paying as tax, since Income Tax Expense (which we get from the Income Statement) already includes any applicable tax refunds from interest payments.

We then update our formula to discount this amount from the true cost of capital for debt:

$$\text{WACC}_\text{debt} = \frac{\text{Interest Expense}}{\text{Total Debt Raised}} * (1 - t)$$

That's it. This is the final form of our $$$\text{WACC}_\text{debt}$$$ formula.³

Example: Calculating $$$\text{WACC}_\text{debt}$$$ for SFIX

Here's an example of how I calculated $$$\text{WACC}_\text{debt}$$$for SFIX:

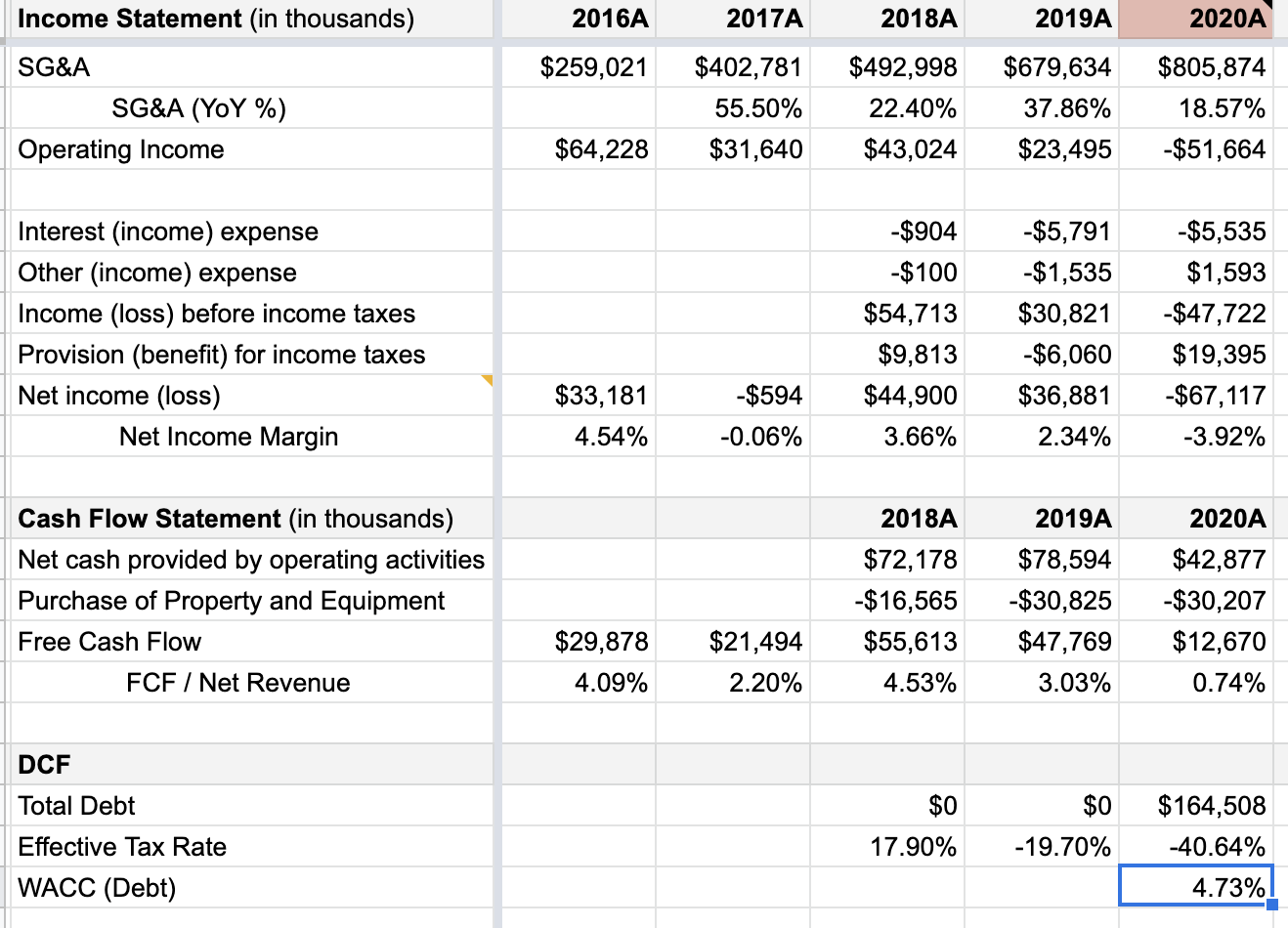
You can access the source 🔗 Google Sheet Valuation Model here

Next up, the slightly more involved process of calculating $$$\text{WACC}_\text{equity}$$$.

Calculating $$$\text{WACC}_\text{equity}$$$

You may be thinking — "Hmm, equity doesn't cost anything. Isn't it just money exchanged for company stock?".

Sure, while that's true in theory, public companies can be traded publicly — and stocks that aren't performing to expectations will get sold off. The process of calculating $$$\text{WACC}_\text{equity}$$$ " inline=truis primarily concerned with capturing this expectation, and reflecting it as the true cost of equity.

Capital Asset Pricing Model

It's important to clarify what we're trying to accomplish here: we want to find a measure for the stocks performance, relative to the performance of the rest of the market.

Stocks matching the performance of the market can be expected to have an 'average' cost of equity. Those that underperform the market will have a higher cost of equity, and those that outperform will have a lower cost of equity.

We arrive at the price using the Capital Asset Pricing Model:

$$\text{WACC}_\text{equity} = R_f + β(\bar{R}_m - R_f)$$

where:

$$$R_f$$$ is the risk-free rate, usually taken to be the value of the Treasury Bond Yield corresponding to your model's period — (5 year bonds if you're modeling 5 years, 10 year bonds if you're modeling 10 years).

$$$β$$$ measures how much a company's share price reacts against the market as a whole. $$$β = 1$$$ indicates that the company moves in line with the market. $$$β > 1$$$ means the share is exaggerating the market's movements; $$$ β < 1$$$ means the share is more stable. You can find the β for a stock online (e.g. SFIX's one here)

$$$(\bar{R}_m - R_f)$$$ is the Equity Market Risk Premium, and it represents the returns investors expect in exchange for them investing in the stock market over and above the risk-free rate.

You'd want $$$\bar{R}_m$$ to represent investor return expectations for the equity market, over some historical period. Over the past 10 years, the S&P500 has provided average returns of ~10%, so you can use that rate. Given the present low interest rate environment (and for the forseeable future), many choose to use lower rates instead — like the pension fund return rate for equities (8.00%)

Example: Calculating $$$\text{WACC}_\text{equity}$$$ for SFIX

To drive this home, let's run through an example on SFIX.

First, let's get the figures we need:

• Treasury Yield 10 Years (^TNX): $$$R_f = 0.93%$$$
• Beta (SFIX): $$$β = 2.37$$$
• Pension fund growth equity returns: $$$\bar{R}_m = 8%$$$

Plugging them into the CAPM formula, we get:

$$\text{WACC}_\text{equity} = R_f + β(\bar{R}_m - R_f)$$

$$\text{WACC}_\text{equity} = 0.0093 + 2.37(0.08 - 0.0093) = 0.1769$$

And there we have it. Our cost of equity is 0.1769, or 17.69%. Notice how the high β has a huge impact on the cost of equity!

Finding the overall WACC

Having found the individual components of $$$\text{WACC}$$$, we can now proceed to combine them, just as we described earlier:

$$\text{WACC}\text{overall} = r\text{equity} * \text{WACC}\text{equity} + r\text{debt} * \text{WACC}_\text{debt}$$

With the values $$$\text{WACC}\text{debt} = 4.73%$$$, $$$\text{WACC}\text{equity} = 17.69%$$$, $$$r_\text{debt} = 2.5%$$$ and $$$r_\text{equity} = 97.5%$$$ … to get:

$$\text{WACC}_\text{overall} = 0.975 * 0.1769 + 0.025 * 0.0473 = 0.1737$$

That's it! The overall cost of capital for $SFIX is 17.37%.

In the next post, we'll learn how to discount future cash flows to the present — using this capital rate.